Introduction to Faraday's Law

Learning Goal:

To understand the terms in Faraday's law for magnetic induction of electric fields, and contrast these fields with those produced

by static charges.

Faraday's law describes how electric fields and electromotive forces are generated from changing magnetic fields. It relates the

line integral of the electric field around a closed loop to the change in the total magnetic field integral across a surface bounded

by that loop:

dem

ε =

=-& J B(r, t).dÃ.

dt

where & = f E(F, t). di is the line integral of the electric field, and the magnetic flux is given by

PM = f B(F, t) dà = f B|da| cos(0).

where is the angle between the magnetic field B and the local normal to the surface bounded by the closed loop.

Direction: The line integral and surface integral reverse their signs if

the reference direction of di or dA is reversed. The right-hand rule

applies here: If the thumb of your right hand points along d.Ã, then the

fingers point along di. You are free to take the loop anywhere you

choose, although usually it makes sense to choose it to lie along the

path of the circuit you are considering.

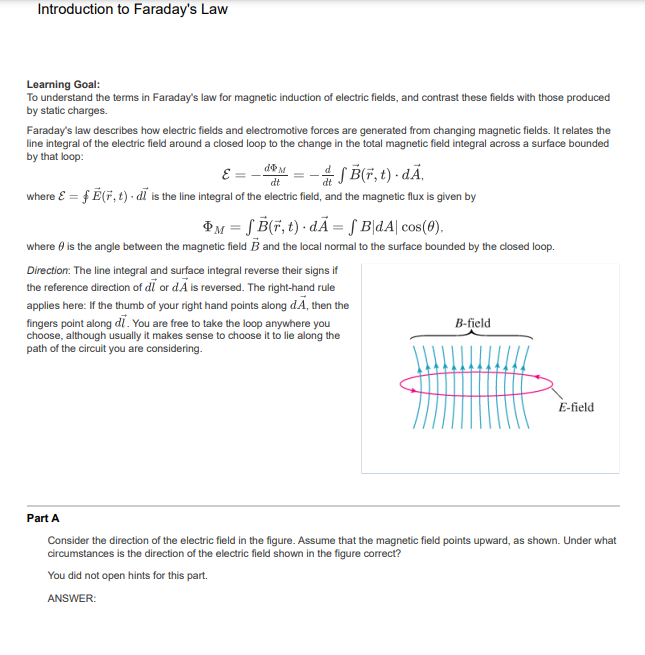
B-field

E-field

Part A

Consider the direction of the electric field in the figure. Assume that the magnetic field points upward, as shown. Under what

circumstances is the direction of the electric field shown in the figure correct?

You did not open hints for this part.

ANSWER:/n7/3/23, 11:21 PM

O

Part B

Now consider the magnetic flux through a surface bounded by the loop. Which of the following statements about this surface

must be true if you want to use Faraday's law to relate the magnetic flux to the line integral of the electric field around the

loop?

ANSWER:

O

Ch 29 HW

always

if B (t) increases with time

if B (t) decreases with time

depending on whether your right thumb is pointing up or down

The surface must be the circular disk in the middle of the loop.

The surface must be perpendicular to the magnetic field at each point.

The surface can be any surface whose edge is the loop.

The surface can be any surface whose edge is the loop as long as no magnetic field line passes through it more

than once.

It is important to understand the vast differences between electric fields produced by changing magnetic fields via Faraday's law

and the more familiar electric fields produced by charges via Coulomb's law. Here are some short questions that illustrate these

differences./nPart C

When can an electric field be measured at any point from the force on a stationary test charge at that point?

You did not open hints for this part.

ANSWER:

only if the field is generated by the coulomb field of static charges

only if the field is generated by a changing magnetic field

no matter how the field is generated/nPart D

When can an electric field that does not vary in time arise?

ANSWER:

7/3/23, 11:21 PM

Ch 29 HW

only if the field is generated by a coulomb field of static charges

only if the field is generated by a changing magnetic field

in either of the above two cases

Electric fields never vary in time; otherwise, a charge could gain energy from the field.

2/23/nPart E

When will the integral & E-di around any closed loop be zero?

ANSWER:

O

only if the field is generated by the coulomb field of static charges

only if the field is generated by the coulomb field of static charges or a constant current

only if the field is generated by a changing magnetic field

however the field is generated

The loop integral is always zero; otherwise, a charge moving around the loop would gain energy.

Here is a simple quantitative problem that uses Faraday's law./nPart F

A cylindrical iron rod of infinite length with cross-sectional area A is oriented with its axis of symmetry coincident with the z

axis of a cylindrical coordinate system as shown in the figure. It has a magnetic field inside that varies according to

B.(t) = Bo + B₁t. Find the theta component Ee(R, t) of the electric field at distance R from the z axis, where R is

larger than the radius of the rod.

Express your answer in terms of A, B, B₁, R, and any

needed constants such as 0,7, and μ40.

You did not open hints for this part.

ANSWER:

7/3/23, 11:21 PM

Ee(R, t) =

Ch 29 HW

R

3/23